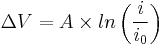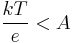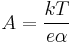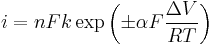Tafel equation
The Tafel equation is an equation in electrochemical kinetics relating the rate of an electrochemical reaction to the overpotential.[1] The Tafel equation was first deduced experimentally and was later shown to have a theoretical justification. The equation is named after German chemist Julius Tafel (1862-1918).
On a single electrode the Tafel equation can be stated as
where
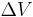 is the overpotential, V
is the overpotential, V is the so called "Tafel slope", V
is the so called "Tafel slope", V is the current density, A/m2 and
is the current density, A/m2 and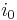 is the so called "exchange current density", A/m2.
is the so called "exchange current density", A/m2.
Contents |
Overview of the terms
The exchange current is the current at equilibrium, i.e. the rate at which oxidized and reduced species transfer electrons with the electrode. In other words, the exchange current density is the rate of reaction at the reversible potential (when the overpotential is zero by definition). At the reversible potential, the reaction is in equilibrium meaning that the forward and reverse reactions progress at the same rates. This rate is the exchange current density.
The Tafel slope is measured experimentally. It, however, can be shown theoretically that when the dominant reaction mechanism involves the transfer of a single electron that
where A is defined as
where
 is Boltzmann's constant,
is Boltzmann's constant, is the absolute temperature,
is the absolute temperature, is the electron charge, and
is the electron charge, and is the so called "charge transfer coefficient", the value of which must be between 0 and 1.
is the so called "charge transfer coefficient", the value of which must be between 0 and 1.
An alternative form
The Tafel equation can be also written as:
where
- the plus sign under the exponent refers to an anodic reaction, and a minus sign to a cathodic reaction,
- n is the number of electrons involved in the electrode reaction
- k is the rate constant for the electrode reaction,
- R is the universal gas constant,
- F is the Faraday constant.
Applicability
Where an electrochemical reaction occurs in two "half reactions" on separate electrodes, the Tafel equation is applied to each electrode separately.
The Tafel equation assumes that the reverse reaction rate is negligible compared to the forward reaction rate.
The Tafel equation is applicable to the region where the values of polarization are high. At low values of polarization, the dependence of current on polarization is usually linear (not logarithmic):
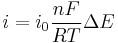 .
.
This linear region is called "polarization resistance" due to its formal similarity to the Ohm's law.
See also
References
- ^ Bard, A. J.; Faulkner, L. R. “Electrochemical Methods. Fundamentals and Applications” 2nd Ed. Wiley, New York. 2001. ISBN 0-471-04372-9
- G.T. Burstein (2005). "A Century of Tafel’s Equation: 1905–2005 A Commemorative Issue of Corrosion Science". Corrosion Science 47 (12): 2858–2870. doi:10.1016/j.corsci.2005.07.002.